Introduction

This is the first article from a series of articles I will be writing about the math behind SVM. There is a lot to talk about and a lot of mathematical backgrounds is often necessary. However, I will try to keep a slow pace and to give in-depth explanations, so that everything is crystal clear, even for beginners.

If you are new and wish to know a little bit more about SVMs before diving into the math, you can read the article: an overview of Support Vector Machine.

---

What is the goal of the Support Vector Machine (SVM)?

The goal of a support vector machine is to find  the optimal separating hyperplane which maximizes the margin of the training data.

The first thing we can see from this definition, is that a SVM needs training data. Which means it is a supervised learning algorithm.

It is also important to know that SVM is a classification algorithm. Which means we will use it to predict if something belongs to a particular class.

For instance, we can have the training data below:

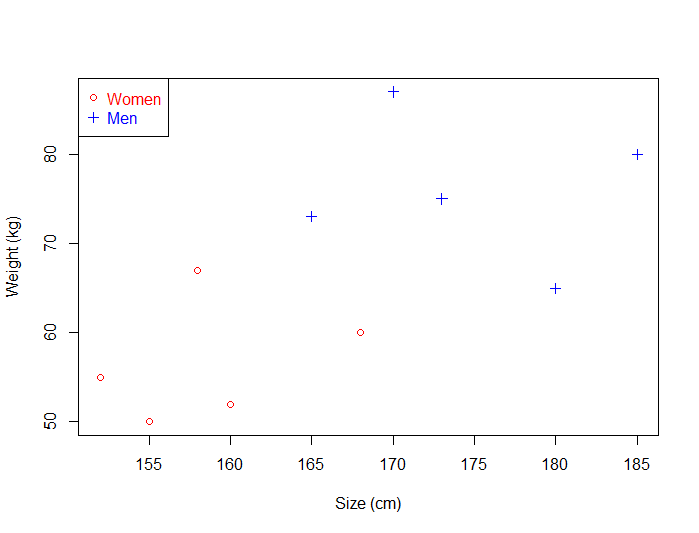
We have plotted the size and weight of several people, and there is also a way to distinguish between men and women.

With such data, using a SVM will allow us to answer the following question:

Given a particular data point (weight and size), is the person a man or a woman ?

For instance:  if someone measures 175 cm and weights 80 kg, is it a man of a woman?

What is a separating hyperplane?

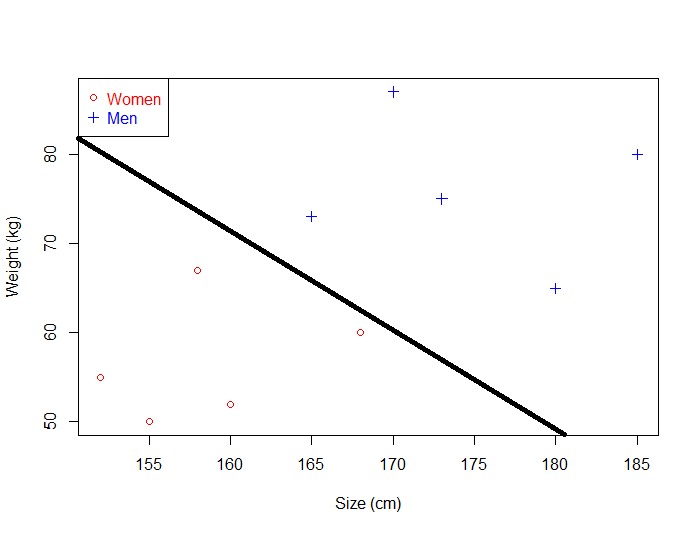
Just by looking at the plot, we can see that it is possible to separate the data.  For instance, we could trace a line and then all the data points representing men will be above the line, and all the data points representing women will be below the line.

Such a line is called a separating hyperplane and is depicted below:

If it is just a line, why do we call it an hyperplane ?

Even though we use a very simple example with data points laying in $R^2$ the support vector machine can work with any number of dimensions !

A hyperplane is a generalization of a plane.

• in one dimension, a hyperplane is called a point
• in two dimensions, it is a line
• in three dimensions, it is a plane
• in more dimensions you can call it an hyperplane

What is the optimal separating hyperplane?

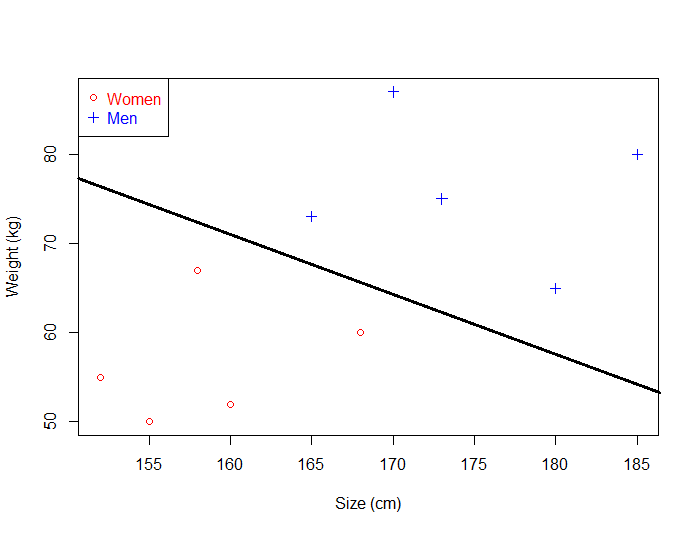
The fact that you can find a separating hyperplane,  does not mean it is the best one !  In the example below there is several separating hyperplanes. Each of them is valid as it successfully separates our data set with men on one side and women on the other side.

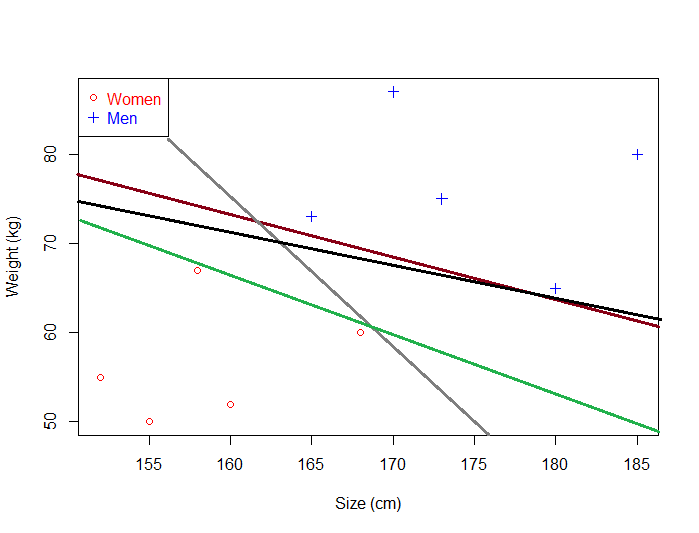
Suppose we select the green hyperplane and use it to classify on real life data.

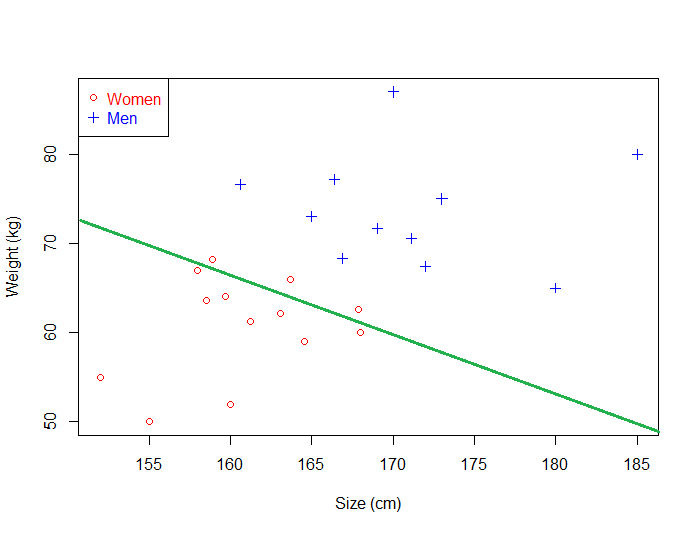
This time, it makes some mistakes as it wrongly classify three women. Intuitively, we can see that if we select an hyperplane which is close to the data points of one class, then it might not generalize well.

So we will try to select an hyperplane as far as possible from data points from each category:

This one looks better. When we use it with real life data, we can see it still make perfect classification.

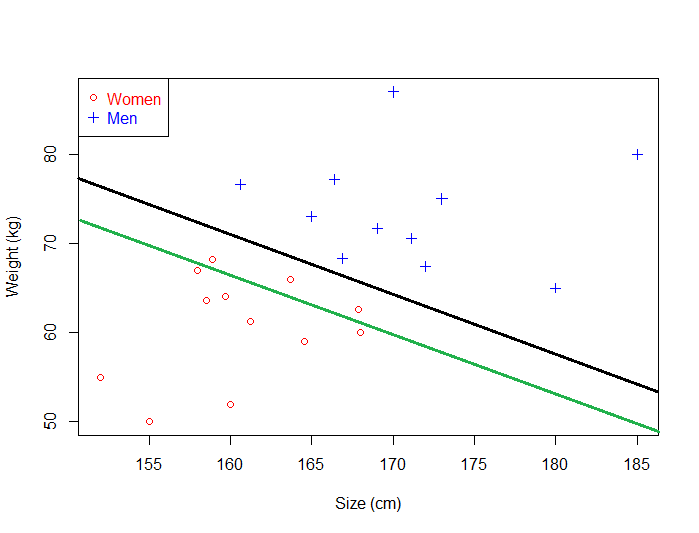
That's why the objective of a SVM is to find the optimal separating hyperplane:

• because it correctly classifies the training data
• and because it is the one which will generalize better with unseen data

What is the margin and how does it help choosing the optimal hyperplane?

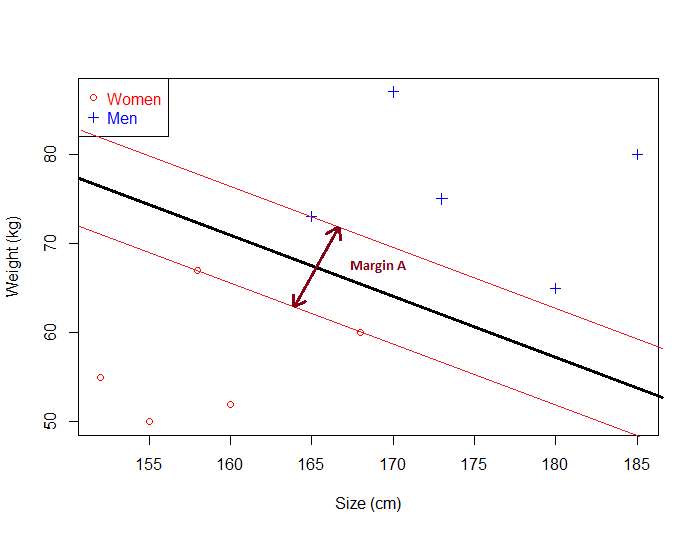
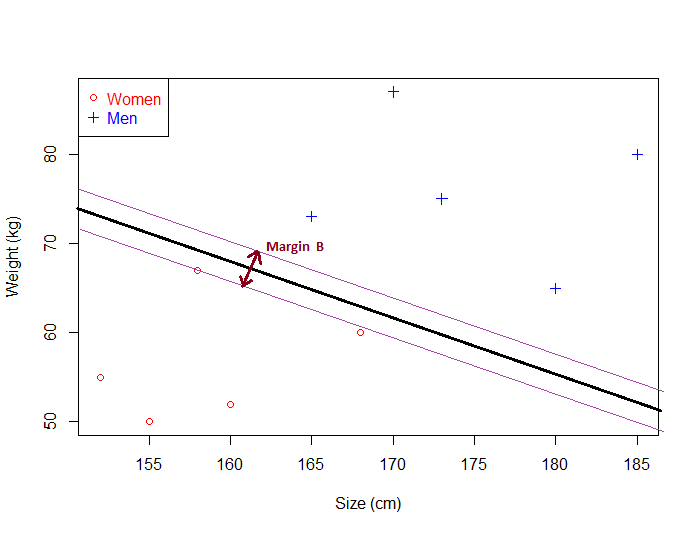
Given a particular hyperplane, we can compute the distance between the hyperplane and the closest data point. Once we have this value, if we double it we will get what is called the margin.

Basically the margin is a no man's land. There will never be any data point inside the margin. (Note: this can cause some problems when data is noisy, and this is why soft margin classifier will be introduced later)

For another hyperplane, the margin will look like this :

As you can see, Margin B is smaller than Margin A.

We can make the following observations:

• If an hyperplane is very close to a data point, its margin will be small.
• The further an hyperplane is from a data point, the larger its margin will be.

This means that the optimal hyperplane will be the one with the biggest margin.

That is why the objective of the SVM is to find  the optimal separating hyperplane which maximizes the margin of the training data.

This concludes this introductory post about the math behind SVM. There was not a lot of formula, but in the next article we will  put on some numbers and try to get the mathematical view of this using geometry and vectors.

If you want to learn more read it now :
SVM - Understanding the math - Part 2 : Calculate the margin