SVM - Understanding the math - the optimal hyperplane

This is the Part 3 of my series of tutorials about the math behind Support Vector Machine.

If you did not read the previous articles, you might want to start the serie at the beginning by reading this article: an overview of Support Vector Machine.

What is this article about?

The main focus of this article is to show you the reasoning allowing us to select the optimal hyperplane.

Here is a quick summary of what we will see:

• How can we find the optimal hyperplane ?
• How do we calculate the distance between two hyperplanes ?
• What is the SVM optimization problem ?

How to find the optimal hyperplane ?

At the end of Part 2 we computed the distance  $\|p\|$ between a point  $A$ and a hyperplane. We then computed the margin which was equal to $2 \|p\|$.

However, even if it did quite a good job at separating the data it was not the optimal hyperplane.

 

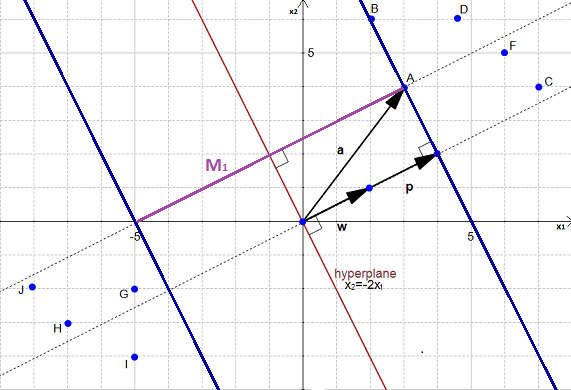
As we saw in Part 1, the optimal hyperplane  is the one which maximizes the margin of the training data.

In Figure 1, we can see that the margin $M_1$, delimited by the two blue lines, is not the biggest margin separating perfectly the data. The biggest margin is the margin $M_2$ shown in Figure 2 below.

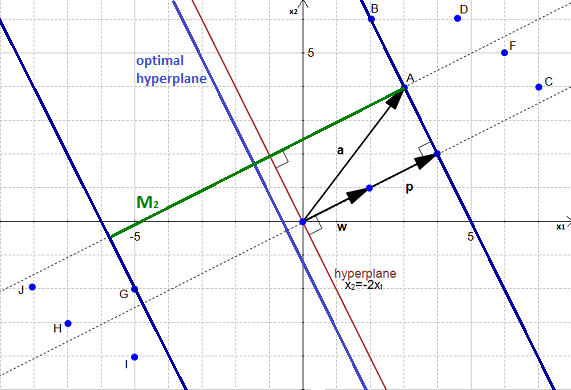
You can also see the optimal hyperplane on Figure 2. It is slightly on the left of our initial hyperplane. How did I find it ? I simply traced a line crossing $M_2$ in its middle.

Right now you should have the feeling that hyperplanes and margins are closely related. And you would be right!

If I have an hyperplane I can compute its margin with respect to some data point. If I have a margin delimited by two hyperplanes (the dark blue lines in Figure 2), I can find a third hyperplane passing right in the middle of the margin.

Finding the biggest margin, is the same thing as finding the optimal hyperplane.

How can we find the biggest margin  ?

It is rather simple:

1. You have a dataset
2. select two hyperplanes which separate the data with no points between them
3. maximize their distance (the margin)

The region bounded by the two hyperplanes will be the biggest possible margin.

If it is so simple why does everybody have so much pain understanding SVM ?
It is because as always the simplicity requires some abstraction and mathematical terminology to be well understood.

So we will now go through this recipe step by step:

Step 1: You have a dataset $\mathcal{D}$ and you want to classify it

Most of the time your data will be composed of $n$ vectors $\mathbf{x}_i$.

Each $\mathbf{x}_i$ will also be associated with a value $y_i$ indicating if the element belongs to the class (+1) or not (-1).

Note that $y_i$  can only have two possible values -1 or +1.

Moreover, most of the time, for instance when you do text classification, your vector $\mathbf{x}_i$ ends up having a lot of dimensions. We can say that $\mathbf{x}_i$ is a $p$-dimensional vector if it has $p$ dimensions.

So your dataset $\mathcal{D}$ is the set of $n$ couples of element $(\mathbf{x}_i, y_i)$

The more formal definition of an initial dataset in set theory is :

$$\mathcal{D} = \left\{ (\mathbf{x}_i, y_i)\mid\mathbf{x}_i \in \mathbb{R}^p,\, y_i \in \{-1,1\}\right\}_{i=1}^n$$

Step 2: You need to select two hyperplanes separating the data with no points between them

Finding two hyperplanes separating some data is easy when you have a pencil and a paper. But with some $p$-dimensional data it becomes more difficult because you can't draw it.

Moreover, even if your data is only 2-dimensional it might not be possible to find a separating hyperplane !

You can only do that if your data is linearly separable

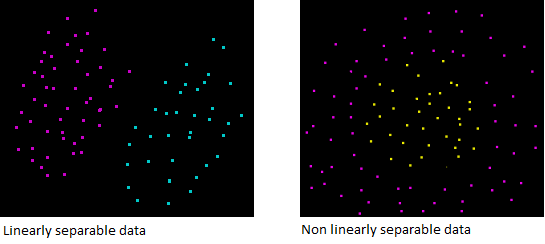
So let's assume that our dataset $\mathcal{D}$ IS linearly separable. We now want to find two hyperplanes with no points between them, but we don't have a way to visualize them.

What do we know about hyperplanes that could help us ?

Taking another look at the hyperplane equation

We saw previously, that the equation of a hyperplane  can be written

$$\mathbf{w}^T\mathbf{x} = 0$$

However, in the Wikipedia article about Support Vector Machine it is said that :

Any hyperplane can be written as the set of points $\mathbf{x}$ satisfying $\mathbf{w}\cdot\mathbf{x}+b=0\$.

First, we recognize another notation for the dot product, the article uses $\mathbf{w}\cdot\mathbf{x}$ instead of  $\mathbf{w}^T\mathbf{x}$.

You might wonder... Where does the $+b$ comes from ? Is our previous definition incorrect ?

Not quite. Once again it is a question of notation. In our definition the vectors $\mathbf{w}$ and $\mathbf{x}$ have three dimensions, while in the Wikipedia definition they have two dimensions:

Given two 3-dimensional vectors $\mathbf{w}(b,-a,1)$ and $\mathbf{x}(1,x,y)$

$$\mathbf{w}\cdot\mathbf{x} = b\times (1) + (-a)\times x + 1 \times y$$

$$\begin{equation}\mathbf{w}\cdot\mathbf{x} = y - ax + b\end{equation}$$

Given two 2-dimensional vectors $\mathbf{w^\prime}(-a,1)$ and $\mathbf{x^\prime}(x,y)$

$$\mathbf{w^\prime}\cdot\mathbf{x^\prime} = (-a)\times x + 1 \times y$$

$$\begin{equation}\mathbf{w^\prime}\cdot\mathbf{x^\prime} = y - ax\end{equation}$$

Now if we add $b$ on both side of the equation $(2)$ we got :

$$\mathbf{w^\prime}\cdot\mathbf{x^\prime} +b = y - ax +b$$

$$\begin{equation}\mathbf{w^\prime}\cdot\mathbf{x^\prime}+b = \mathbf{w}\cdot\mathbf{x}\end{equation}$$

For the rest of this article we will use 2-dimensional vectors (as in equation (2)).

Given a hyperplane $H_0$ separating the dataset and satisfying:

$$\mathbf{w}\cdot\mathbf{x} + b=0\$$

We can select two others hyperplanes $H_1$ and $H_2$ which also separate the data and have the following equations :

$$\mathbf{w}\cdot\mathbf{x} + b=\delta\$$

and

$$\mathbf{w}\cdot\mathbf{x} + b=-\delta\$$

so that $H_0$ is equidistant from $H_1$ and $H_2$.

However, here the variable $\delta$ is not necessary. So we can set $\delta=1$ to simplify the problem.

$$\mathbf{w}\cdot\mathbf{x} + b=1\$$

and

$$\mathbf{w}\cdot\mathbf{x} + b=-1\$$

Now we want to be sure that they have no points between them.

We won't select any hyperplane, we will only select those who meet the two following constraints:

For each vector $\mathbf{x_i}$ either :

$$\begin{equation}\mathbf{w}\cdot\mathbf{x_i} + b \geq 1\;\text{for }\;\mathbf{x_i}\;\text{having the class}\;1\end{equation}$$

or

$$\begin{equation}\mathbf{w}\cdot\mathbf{x_i} + b \leq -1\;\text{for }\;\mathbf{x_i}\;\text{having the class}\;-1\end{equation}$$

Understanding the constraints

On the following figures, all red points have the class $1$ and all blue points have the class $-1$.

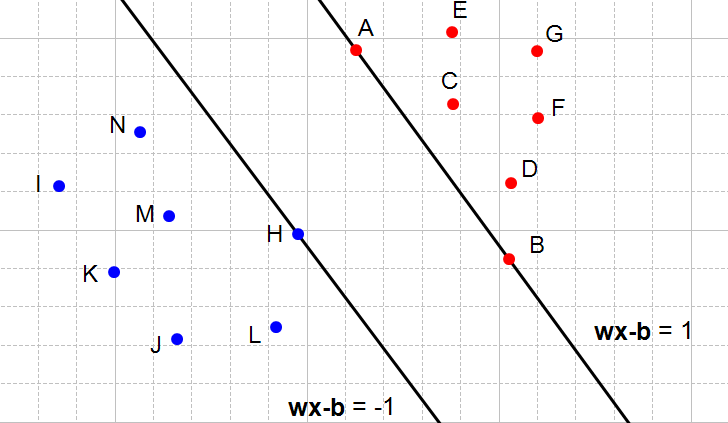
So let's look at Figure 4 below and consider the point $A$. It is red so it has the class $1$ and we need to verify it does not violate the constraint $\mathbf{w}\cdot\mathbf{x_i} + b \geq1\$

When $\mathbf{x_i} = A$  we see that the point is on the hyperplane so $\mathbf{w}\cdot\mathbf{x_i} + b =1\$ and the constraint is respected. The same applies for $B$.

When $\mathbf{x_i} = C$  we see that the point is above the hyperplane so $\mathbf{w}\cdot\mathbf{x_i} + b >1\$ and the constraint is respected. The same applies for $D$, $E$, $F$ and $G$.

With an analogous reasoning you should find that the second constraint is respected for the class $-1$.

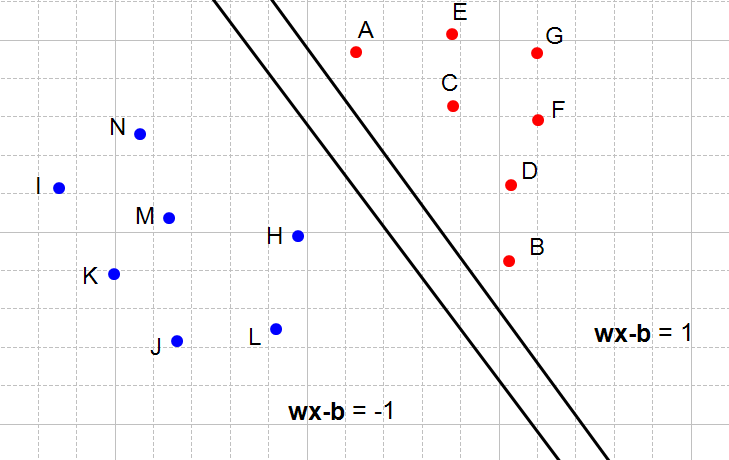
On Figure 5, we see another couple of hyperplanes respecting the constraints:

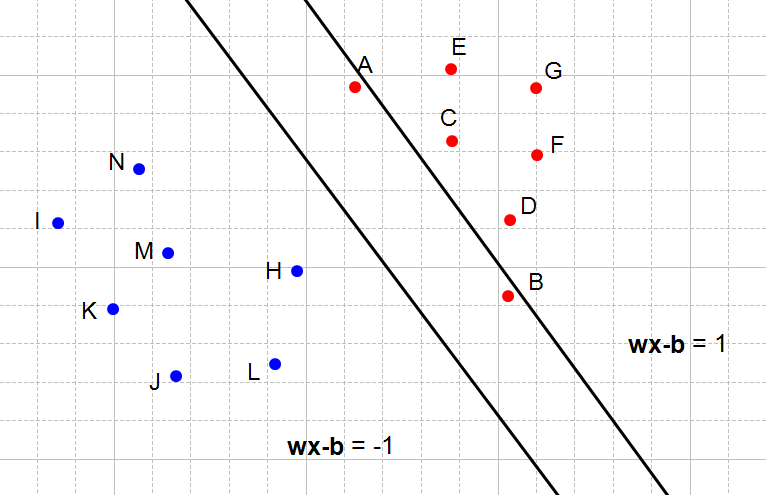
And now we will examine cases where the constraints are not respected:

 

 

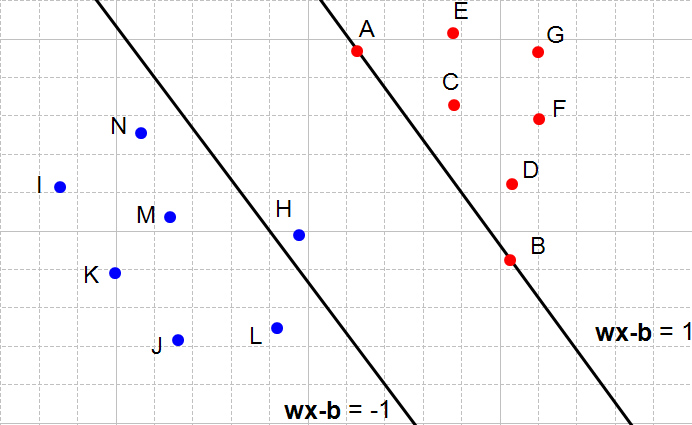
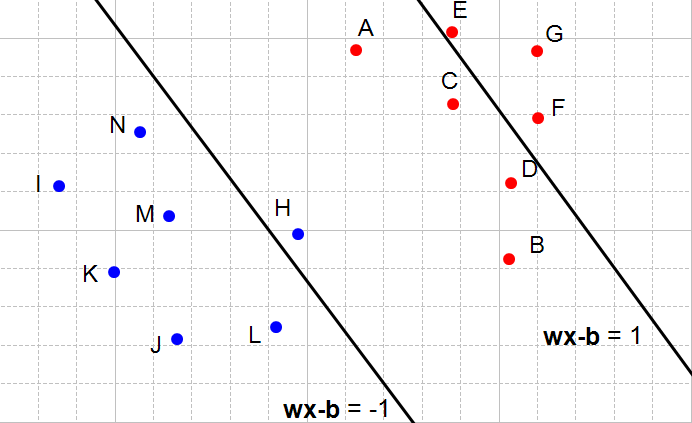
What does it means when a constraint is not respected ? It means that we cannot select these two hyperplanes. You can see that every time the constraints are not satisfied (Figure 6, 7 and 8) there are points between the two hyperplanes.

By defining these constraints, we found a way to reach our initial goal of selecting two hyperplanes without points between them.  And it works not only in our examples but also in $p$-dimensions !

Combining both constraints

In mathematics, people like things to be expressed concisely.

Equations (4) and (5) can be combined into a single constraint:

We start with equation (5)

$$\text{for }\;\mathbf{x_i}\;\text{having the class}\;-1$$

$$\mathbf{w}\cdot\mathbf{x_i}+b \leq -1$$

And multiply both sides by $y_i$ (which is always -1 in this equation)

$$y_i(\mathbf{w}\cdot\mathbf{x_i}+b ) \geq y_i(-1)$$

Which means equation (5) can also be written:

$$\begin{equation}y_i(\mathbf{w}\cdot\mathbf{x_i} + b ) \geq 1\end{equation}\;\text{for }\;\mathbf{x_i}\;\text{having the class}\;-1$$

In equation (4), as $y_i =1$ it doesn't change the sign of the inequation.

$$\begin{equation}y_i(\mathbf{w}\cdot\mathbf{x_i} + b) \geq 1\;\text{for }\;\mathbf{x_i}\;\text{having the class}\;1\end{equation}$$

We combine equations (6) and (7) :

$$\begin{equation}y_i(\mathbf{w}\cdot\mathbf{x_i} + b) \geq 1\;\text{for all}\;1\leq i \leq n\end{equation}$$

We now have a unique constraint (equation 8) instead of two (equations 4 and 5) , but they are mathematically equivalent. So their effect is the same (there will be no points between the two hyperplanes).

Step 3: Maximize the distance between the two hyperplanes

This is probably be the hardest part of the problem. But don't worry, I will explain everything along the way.

a) What is the distance between our two hyperplanes ?

Before trying to maximize the distance between the two hyperplane, we will first ask ourselves: how do we compute it ?

Let:

• $\mathcal{H}_0$ be the hyperplane having the equation $\textbf{w}\cdot\textbf{x} + b = -1$
• $\mathcal{H}_1$ be the hyperplane having the equation $\textbf{w}\cdot\textbf{x} + b = 1$
• $\textbf{x}_0$ be a point in the hyperplane $\mathcal{H}_0$.

We will call $m$ the perpendicular distance from $\textbf{x}_0$ to the hyperplane $\mathcal{H}_1$ . By definition, $m$ is what we are used to call the margin.

As $\textbf{x}_0$ is in $\mathcal{H}_0$, $m$ is the distance between hyperplanes $\mathcal{H}_0$ and $\mathcal{H}_1$ .

We will now try to find the value of $m$.

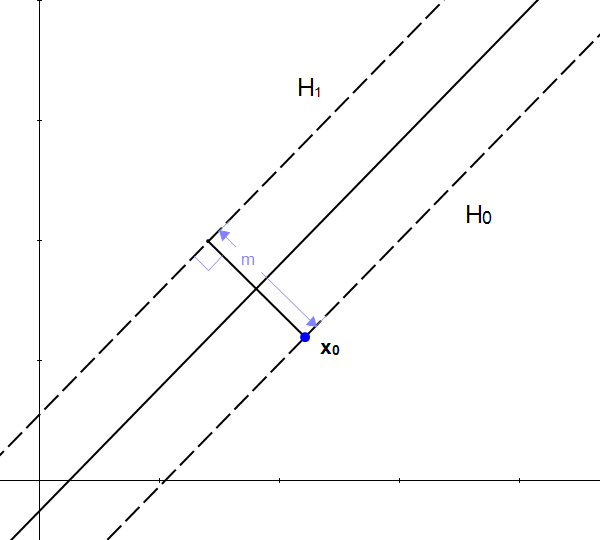
You might be tempted to think that if we add $m$ to $\textbf{x}_0$ we will get another point, and this point will be on the other hyperplane !

But it does not work, because $m$ is a scalar, and $\textbf{x}_0$ is a vector and adding a scalar with a vector is not possible. However, we know that adding two vectors is possible, so if we transform $m$ into a vector we will be able to do an addition.

We can find the set of all points which are at a distance $m$ from  $\textbf{x}_0$. It can be represented as a circle :

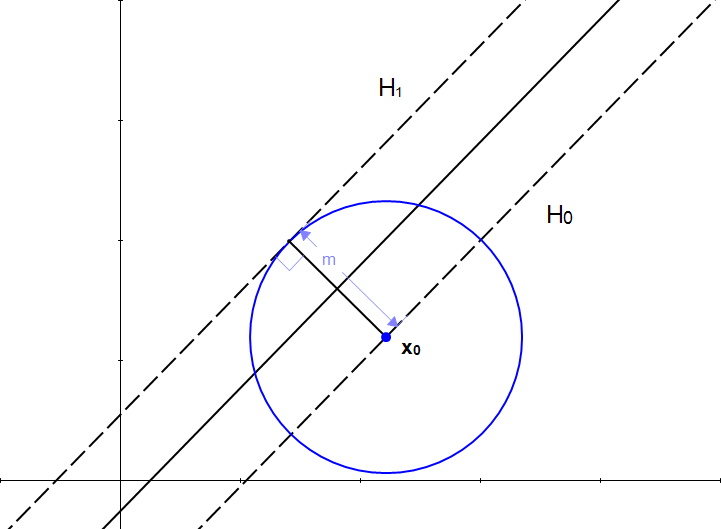
Looking at the picture, the necessity of a vector become clear. With just the length $m$ we don't have one crucial information : the direction. (recall from Part 2 that a vector has a magnitude and a direction).

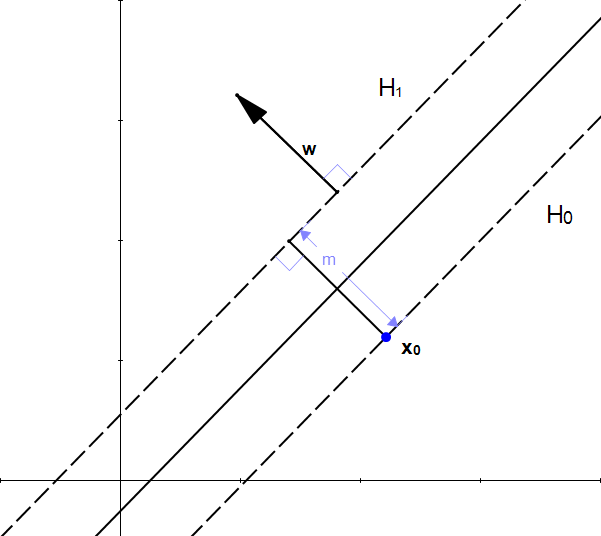
We can't add a scalar to a vector, but we know if we multiply a scalar with a vector we will get another vector.

From our initial statement, we want  this vector:

1. to have a magnitude of $m$
2. to be perpendicular to the hyperplane $\mathcal{H}_1$

Fortunately, we already know a vector perpendicular to $\mathcal{H}_1$, that is $\textbf{w}$ (because  $\mathcal{H}_1 = \textbf{w}\cdot\textbf{x} + b = 1$)

Let's define $\textbf{u} = \frac{\textbf{w}}{\|\textbf{w}\|}$ the unit vector of $\textbf{w}$. As it is a unit vector $\|\textbf{u}\| = 1$ and it has the same direction as $\textbf{w}$ so it is also perpendicular to the hyperplane.

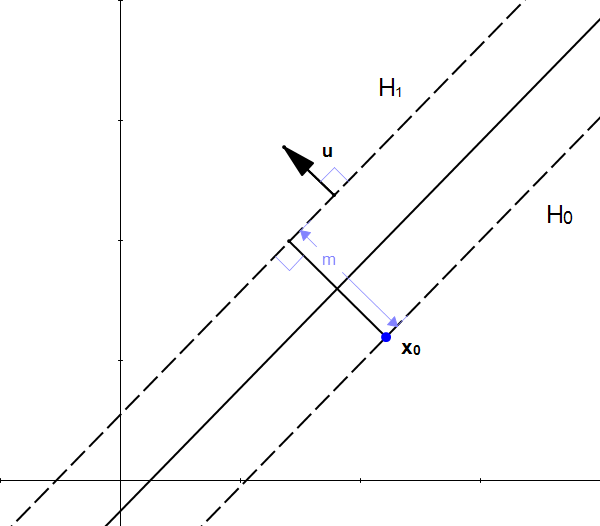
If we multiply $\textbf{u}$ by $m$ we get the vector $\textbf{k} = m\textbf{u}$ and :

1. $\|\textbf{k}\| = m$
2. $\textbf{k}$ is perpendicular to $\mathcal{H}_1$ (because it has the same direction as $\textbf{u}$)

From these properties we can see that $\textbf{k}$ is the vector we were looking for.

$$\begin{equation}\textbf{k}=m\textbf{u}=m\frac{\textbf{w}}{\|\textbf{w}\|}\end{equation}$$

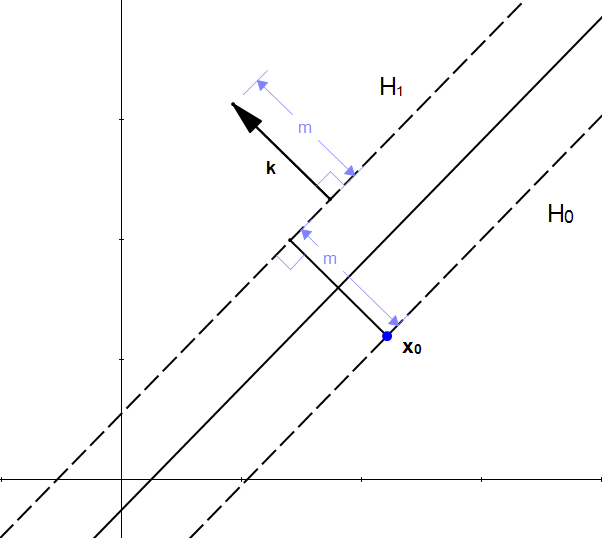
We did it ! We transformed our scalar $m$ into a vector $\textbf{k}$ which we can use to perform an addition with the vector $\textbf{x}_0$.

If we start from the point $\textbf{x}_0$ and add $k$ we find that the point $\textbf{z}_0 = \textbf{x}_0 + \textbf{k}$ is in the hyperplane $\mathcal{H}_1$  as shown on Figure 14.

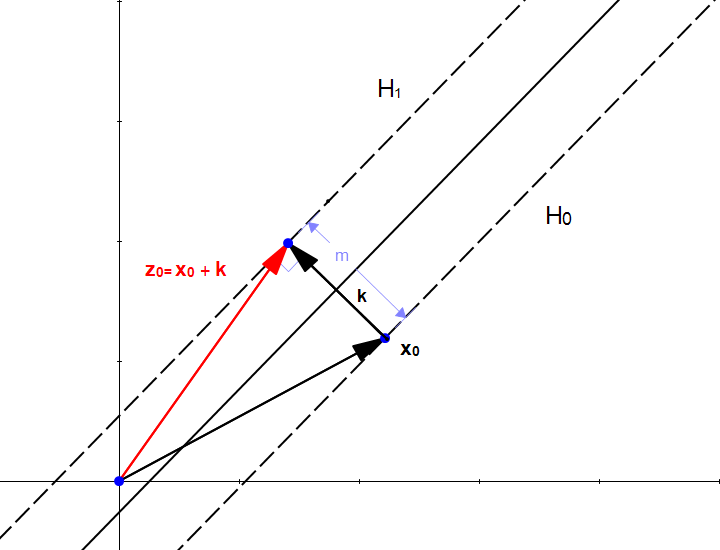
The fact that $\textbf{z}_0$ is in $\mathcal{H}_1$ means that

$$\begin{equation}\textbf{w}\cdot\textbf{z}_0+b = 1\end{equation}$$

We can replace $\textbf{z}_0$ by $\textbf{x}_0+\textbf{k}$ because that is how we constructed it.

$$\begin{equation}\textbf{w}\cdot(\textbf{x}_0+\textbf{k})+b = 1\end{equation}$$

We can now replace $\textbf{k}$ using equation $(9)$

$$\begin{equation}\textbf{w}\cdot(\textbf{x}_0+m\frac{\textbf{w}}{\|\textbf{w}\|})+b = 1\end{equation}$$

We now expand equation $(12)$

$$\begin{equation}\textbf{w}\cdot\textbf{x}_0 +m\frac{\textbf{w}\cdot\textbf{w}}{\|\textbf{w}\|}+b = 1\end{equation}$$

The dot product of a vector with itself is the square of its norm so :

$$\begin{equation}\textbf{w}\cdot\textbf{x}_0 +m\frac{\|\textbf{w}\|^2}{\|\textbf{w}\|}+b = 1\end{equation}$$

$$\begin{equation}\textbf{w}\cdot\textbf{x}_0 +m\|\textbf{w}\|+b = 1\end{equation}$$

$$\begin{equation}\textbf{w}\cdot\textbf{x}_0 +b = 1 - m\|\textbf{w}\|\end{equation}$$

As $\textbf{x}_0$ is in $\mathcal{H}_0$ then $\textbf{w}\cdot\textbf{x}_0 +b = -1$

$$\begin{equation} -1= 1 - m\|\textbf{w}\|\end{equation}$$

$$\begin{equation} m\|\textbf{w}\|= 2\end{equation}$$

$$\begin{equation} m = \frac{2}{\|\textbf{w}\|}\end{equation}$$

This is it ! We found a way to compute $m$.

b) How to maximize the distance between our two hyperplanes

We now have a formula to compute the margin:

$$m= \frac{2}{\|\textbf{w}\|}$$

The only variable we can change in this formula is the norm of  $\mathbf{w}$.

Let's try to give it different values:

When $\|\textbf{w}\|=1$ then $m=2$

When $\|\textbf{w}\|=2$ then $m=1$

When $\|\textbf{w}\|=4$ then $m=\frac{1}{2}$

One can easily see that the bigger the norm is, the smaller the margin become.

Maximizing the margin is the same thing as minimizing the norm of $\textbf{w}$

Our goal is to maximize the margin. Among all possible hyperplanes meeting the constraints,  we will choose the hyperplane with the smallest $\|\textbf{w}\|$ because it is the one which will have the biggest margin.

This give us the following optimization problem:

Minimize in ($\textbf{w}, b$)

$\|\textbf{w}\|$

subject to $y_i(\mathbf{w}\cdot\mathbf{x_i}+b) \geq 1$

(for any $i = 1, \dots, n$)

Solving this problem is like solving and equation. Once we have solved it, we will have found the couple ($\textbf{w}, b$)  for which $\|\textbf{w}\|$ is the smallest possible and the constraints we fixed are met. Which means we will have the equation of the optimal hyperplane !

Conclusion

We discovered that finding the optimal hyperplane requires us to solve an optimization problem.  Optimization problems are themselves somewhat tricky. And you need more background information to be able to solve them.  So we will go step by step. Let us discover unconstrained minimization problems in Part 4! Thanks for reading.