
Today we are going to talk about SVMs in general.
I recently received an email from a reader of my serie of articles about the math behind SVM:
I felt I got deviated a lot on Math part and its derivations and assumptions and finally got confused what exactly SVM is ? And when to use it and how it helps ?
What exactly is SVM ?
SVM is a supervised learning model
It means you need a dataset which has been labeled.
Exemple: I have a business and I receive a lot of emails from customers every day. Some of these emails are complaints and should be answered very quickly. I would like a way to identify them quickly so that I answer these email in priority.
Approach 1: I can create a label in gmail using keywords, for instance "urgent", "complaint", "help"
The drawback of this method is that I need to think of all potential keywords that some angry users might use, and I will probably miss some of them. Over time, my keyword list will probably become very messy and it will be hard to maintain.
Approach 2: I can use a supervised machine learning algorithm.
Step 1: I need a lot of emails, the more the better.
Step 2: I will read the title of each email and classify it by saying "it is a complaint" or "it is not a complaint". It put a label on each email.
Step 3: I will train a model on this dataset
Step 4: I will assess the quality of the prediction (using cross validation)
Step 5: I will use this model to predict if an email is a complaint or not.
In this case, if I have trained the model with a lot of emails then it will perform well. SVM is just one among many models you can use to learn from this data and make predictions.
Note that the crucial part is Step 2. If you give SVM unlabeled emails, then it can do nothing.
SVM learns a linear model
Now we saw in our previous example that at the Step 3 a supervised learning algorithm such as SVM is trained with the labeled data. But what is it trained for? It is trained to learn something.
What does it learn?
In the case of SVM, it learns a linear model.
What is a linear model? In simple words: it is a line (in complicated words it is a hyperplane).
If your data is very simple and only has two dimensions, then the SVM will learn a line which will be able to separate the data.
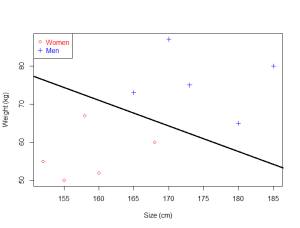
If it is just a line, why do we talk about a linear model?
Because you cannot learn a line.
So instead of that:
- 1) We suppose that the data we want to classify can be separated by a line
- 2) We know that a line can be represented by the equation
 (this is our model)
(this is our model) - 3) We know that there is an infinity of possible lines obtained by changing the value of
 and
and 
- 4) We use an algorithm to determine which are the values of
 and
and  giving the "best" line separating the data.
giving the "best" line separating the data.
SVM is one of these algorithms.
Algorithm or model?
At the start of the article I said SVM is a supervised learning model, and now I say it is an algorithm. What's wrong? The term algorithm is often loosely used. For instance, you will sometime read that SVM is a supervised learning algorithm. This is not true if you consider that an algorithm is a set of actions to perform to obtain a specific result. Sequential minimal optimization is the most used algorithm to train SVM, but you can train an SVM with another algorithm like Coordinate descent. However, most people are not interested in details like this, so we simplify and say that we use the SVM "algorithm" (without saying in details which one we use).
SVM or SVMs?
Sometime, you will see people talk about SVM, and sometime about SVMs.
As often Wikipedia is quite good at stating things clearly:
In machine learning, support vector machines (SVMs) are supervised learning models with associated learning algorithms that analyze data used for classification and regression analysis. (Wikipedia)
So, we now discover that there are several models, which belongs to the SVM family.
SVMs - Support Vector Machines
Wikipedia tells us that SVMs can be used to do two things: classification or regression.
- SVM is used for classification
- SVR (Support Vector Regression) is used for regression
So it makes sense to say that there are several Support Vector Machines. However, this is not the end of the story !
Classification
In 1957, a simple linear model called the Perceptron was invented by Frank Rosenblatt to do classification (which is in fact one of the building block of simple neural networks also called Multilayer Perceptron).
A few years later, Vapnik and Chervonenkis, proposed another model called the "Maximal Margin Classifier", the SVM was born.
Then, in 1992, Vapnik et al. had the idea to apply what is called the Kernel Trick, which allow to use the SVM to classify linearly nonseparable data.
Eventually, in 1995, Cortes and Vapnik introduced the Soft Margin Classifier which allows us to accept some misclassifications when using a SVM.
So just when we talk about classification there is already four different Support Vector Machines:
- The original one : the Maximal Margin Classifier,
- The kernelized version using the Kernel Trick,
- The soft-margin version,
- The soft-margin kernelized version (which combine 1, 2 and 3)
And this is of course the last one which is used most of the time. That is why SVMs can be tricky to understand at first, because they are made of several pieces which came with time.
That is why when you use a programming language you are often asked to specify which kernel you want to use (because of the kernel trick), and which value of the hyperparameter C you want to use (because it controls the effect of the soft-margin).
Regression
In 1996, Vapnik et al. proposed a version of SVM to perform regression instead of classification. It is called Support Vector Regression (SVR). Like the classification SVM, this model includes the C hyperparameter and the kernel trick.
I wrote a simple article, explaining how to use SVR in R.
If you wish to learn more about SVR, you can read this good tutorial by Smola and Schölkopft.
Summary of the history
- Maximal Margin Classifier (1963 or 1979)
- Kernel Trick (1992)
- Soft Margin Classifier (1995)
- Support Vector Regression (1996)
If you want to know more, you can learn this very detailed overview of the history.
Other type of Support Vector Machines
Because SVMs have been very successful at classification, people started to think about using the same logic for other type of problems, or to create derivation. As a result there exists now several different and interesting methods in the SVM family:
- Structured support vector machine which is able to predict structured objects
- Least square support vector machine used for classification and regression
- Support vector clustering used to perform cluster analysis
- Transductive Support Vector Machine used for semi-supervised learning
- Ranking SVM used to sort results
- One class support vector machine used for anomaly detection
Conclusion
We have learned that it is normal to have some difficulty to understand what SVM is exactly. This is because there are several Support Vector Machines used for different purposes. As often, history allows us to have a better vision of how the SVM we know today has been built.
I hope this article give you a broader view of the SVM panorama, and will allow you to understand these machines better.
If you wish to learn more about how SVM work for classification, you can start reading the math series:
SVM - Understanding the math
Part 1: What is the goal of the Support Vector Machine (SVM)?
Part 2: How to compute the margin?
Part 3: How to find the optimal hyperplane?
Part 4: Unconstrained minimization
Part 5: Convex functions
Part 6: Duality and Lagrange multipliers
I am passionate about machine learning and Support Vector Machine. I like to explain things simply to share my knowledge with people from around the world.