This is the Part 3 of my series of tutorials about the math behind Support Vector Machine.
If you did not read the previous articles, you might want to start the serie at the beginning by reading this article: an overview of Support Vector Machine.
What is this article about?
The main focus of this article is to show you the reasoning allowing us to select the optimal hyperplane.
Here is a quick summary of what we will see:
- How can we find the optimal hyperplane ?
- How do we calculate the distance between two hyperplanes ?
- What is the SVM optimization problem ?
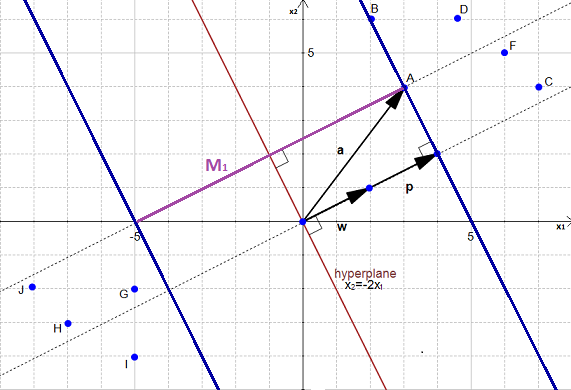
How to find the optimal hyperplane ?
At the end of Part 2 we computed the distance  between a point
between a point  and a hyperplane. We then computed the margin which was equal to
and a hyperplane. We then computed the margin which was equal to  .
.
However, even if it did quite a good job at separating the data it was not the optimal hyperplane.
I am passionate about machine learning and Support Vector Machine. I like to explain things simply to share my knowledge with people from around the world.