
This is Part 2 of my series of tutorial about the math behind Support Vector Machines.
If you did not read the previous article, you might want to start the serie at the beginning by reading this article: an overview of Support Vector Machine.
In the first part, we saw what is the aim of the SVM. Its goal is to find the hyperplane which maximizes the margin.
But how do we calculate this margin?
SVM = Support VECTOR Machine
In Support Vector Machine, there is the word vector.
That means it is important to understand vector well and how to use them.
Here a short sum-up of what we will see today:
- What is a vector?
- its norm
- its direction
- How to add and subtract vectors ?
- What is the dot product ?
- How to project a vector onto another ?
Once we have all these tools in our toolbox, we will then see:
- What is the equation of the hyperplane?
- How to compute the margin?
What is a vector?
If we define a point  in
in  we can plot it like this.
we can plot it like this.
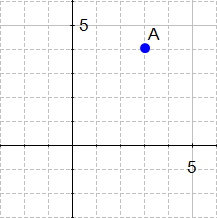
Definition: Any point
, in
specifies a vector in the plane, namely the vector starting at the origin and ending at x.
This definition means that there exists a vector between the origin and A.
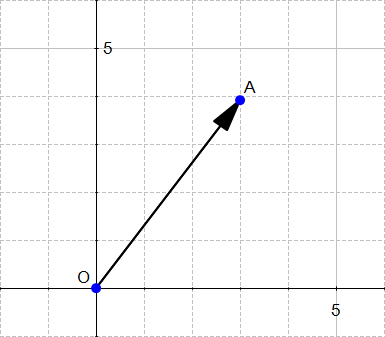
If we say that the point at the origin is the point  then the vector above is the vector
then the vector above is the vector  . We could also give it an arbitrary name such as
. We could also give it an arbitrary name such as  .
.
Note: You can notice that we write vector either with an arrow on top of them, or in bold, in the rest of this text I will use the arrow when there is two letters like  and the bold notation otherwise.
and the bold notation otherwise.
Ok so now we know that there is a vector, but we still don't know what IS a vector.
Definition: A vector is an object that has both a magnitude and a direction.
We will now look at these two concepts.
1) The magnitude
The magnitude or length of a vector  is written
is written  and is called its norm.
and is called its norm.
For our vector  ,
,  is the length of the segment
is the length of the segment 
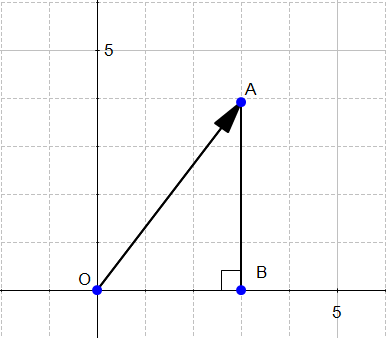
From Figure 3 we can easily calculate the distance OA using Pythagoras' theorem:





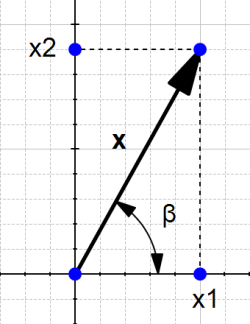
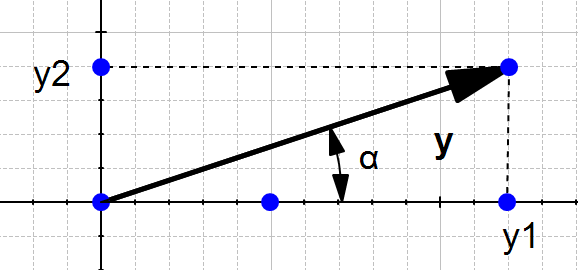
2) The direction
The direction is the second component of a vector.
Definition : The direction of a vector
is the vector
Where does the coordinates of  come from ?
come from ?
Understanding the definition
To find the direction of a vector, we need to use its angles.
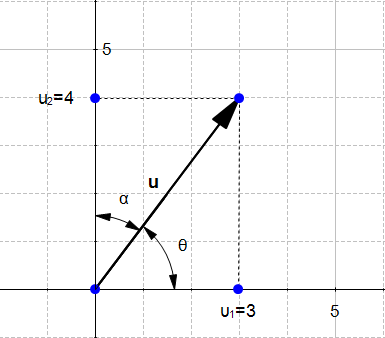
Figure 4 displays the vector  with
with  and
and 
We could say that :
Naive definition 1: The direction of the vector  is defined by the angle
is defined by the angle  with respect to the horizontal axis, and with the angle
with respect to the horizontal axis, and with the angle  with respect to the vertical axis.
with respect to the vertical axis.
This is tedious. Instead of that we will use the cosine of the angles.
In a right triangle, the cosine of an angle  is defined by :
is defined by :

In Figure 4 we can see that we can form two right triangles, and in both case the adjacent side will be on one of the axis. Which means that the definition of the cosine implicitly contains the axis related to an angle. We can rephrase our naïve definition to :
Naive definition 2: The direction of the vector  is defined by the cosine of the angle
is defined by the cosine of the angle  and the cosine of the angle
and the cosine of the angle  .
.
Now if we look at their values :


Hence the original definition of the vector  . That's why its coordinates are also called direction cosine.
. That's why its coordinates are also called direction cosine.
Computing the direction vector
We will now compute the direction of the vector  from Figure 4.:
from Figure 4.:

and

The direction of  is the vector
is the vector 
If we draw this vector we get Figure 5:
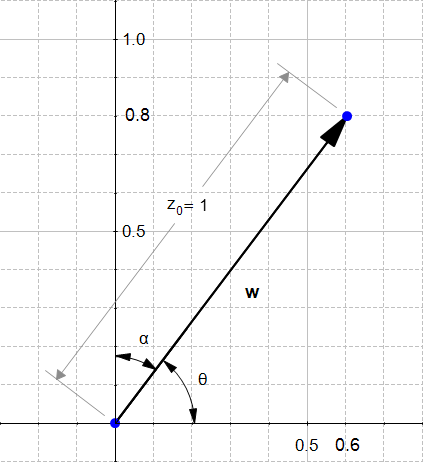
We can see that  as indeed the same look as
as indeed the same look as  except it is smaller. Something interesting about direction vectors like
except it is smaller. Something interesting about direction vectors like  is that their norm is equal to 1. That's why we often call them unit vectors.
is that their norm is equal to 1. That's why we often call them unit vectors.
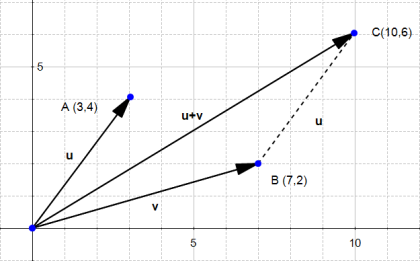
The sum of two vectors
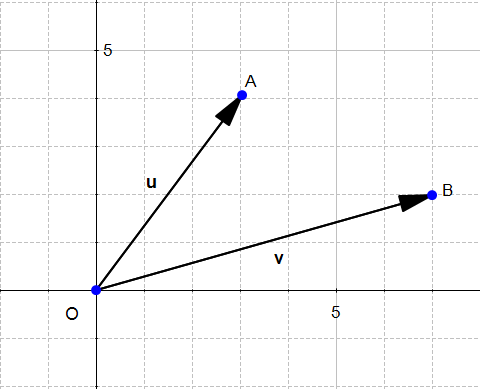
Given two vectors  and
and  then :
then :

Which means that adding two vectors gives us a third vector whose coordinate are the sum of the coordinates of the original vectors.
You can convince yourself with the example below:
The difference between two vectors
The difference works the same way :

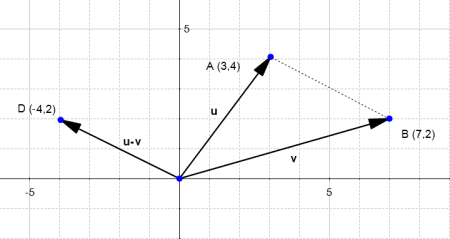
Since the subtraction is not commutative, we can also consider the other case:

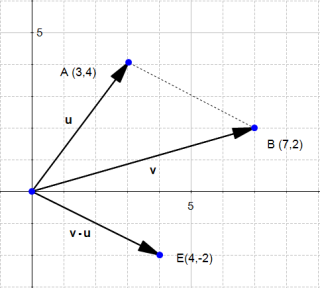
The last two pictures describe the "true" vectors generated by the difference of  and
and  .
.
However, since a vector has a magnitude and a direction, we often consider that parallel translate of a given vector (vectors with the same magnitude and direction but with a different origin) are the same vector, just drawn in a different place in space.
So don't be surprised if you meet the following :
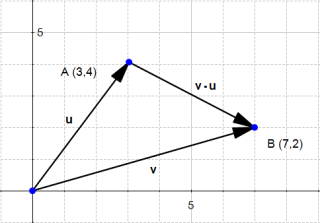
and
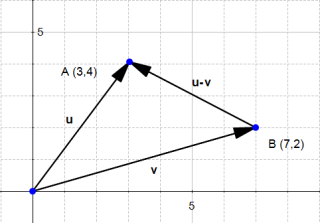
If you do the math, it looks wrong, because the end of the vector  is not in the right point, but it is a convenient way of thinking about vectors which you'll encounter often.
is not in the right point, but it is a convenient way of thinking about vectors which you'll encounter often.
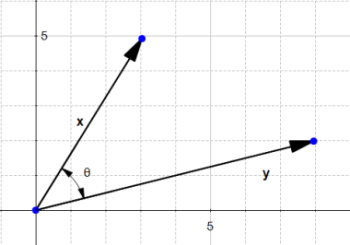
The dot product
One very important notion to understand SVM is the dot product.
Definition: Geometrically, it is the product of the Euclidian magnitudes of the two vectors and the cosine of the angle between them
Which means if we have two vectors  and
and  and there is an angle
and there is an angle  (theta) between them, their dot product is :
(theta) between them, their dot product is :

Why ?
To understand let's look at the problem geometrically.
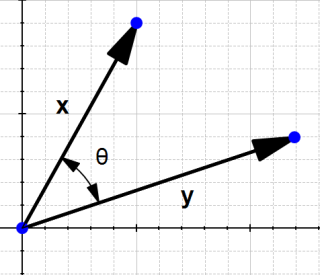
In the definition, they talk about  , let's see what it is.
, let's see what it is.
By definition we know that in a right-angled triangle:

In our example, we don't have a right-angled triangle.
However if we take a different look Figure 12 we can find two right-angled triangles formed by each vector with the horizontal axis.
and
So now we can view our original schema like this:
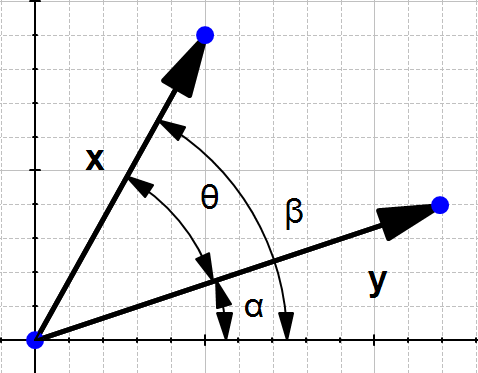
We can see that

So computing  is like computing
is like computing 
There is a special formula called the difference identity for cosine which says that:

(if you want you can read the demonstration here)
Let's use this formula!




So if we replace each term



If we multiply both sides by  we get:
we get:

Which is the same as :

We just found the geometric definition of the dot product !
Eventually from the two last equations we can see that :

This is the algebraic definition of the dot product !
A few words on notation
The dot product is called like that because we write a dot between the two vectors.
Talking about the dot product  is the same as talking about
is the same as talking about
- the inner product
 (in linear algebra)
(in linear algebra) - scalar product because we take the product of two vectors and it returns a scalar (a real number)
The orthogonal projection of a vector
Given two vectors  and
and  , we would like to find the orthogonal projection of
, we would like to find the orthogonal projection of  onto
onto  .
.
To do this we project the vector  onto
onto 
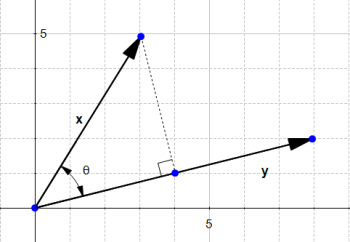
This give us the vector 
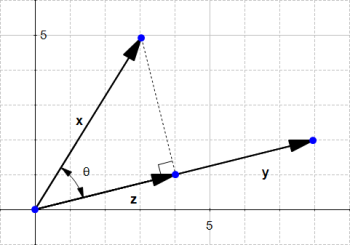
By definition :


We saw in the section about the dot product that

So we replace  in our equation:
in our equation:


If we define the vector  as the direction of
as the direction of  then
then

and

We now have a simple way to compute the norm of the vector  .
.
Since this vector is in the same direction as  it has the direction
it has the direction 


And we can say :
The vector
is the orthogonal projection of
onto
.
Why are we interested by the orthogonal projection ? Well in our example, it allows us to compute the distance between  and the line which goes through
and the line which goes through  .
.
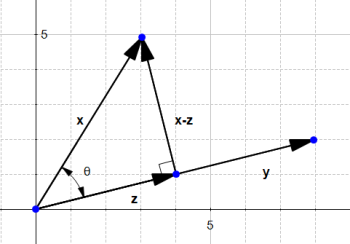
We see that this distance is 

The SVM hyperplane
Understanding the equation of the hyperplane
You probably learnt that an equation of a line is :  . However when reading about hyperplane, you will often find that the equation of an hyperplane is defined by :
. However when reading about hyperplane, you will often find that the equation of an hyperplane is defined by :

How does these two forms relate ?
In the hyperplane equation you can see that the name of the variables are in bold. Which means that they are vectors ! Moreover,  is how we compute the inner product of two vectors, and if you recall, the inner product is just another name for the dot product !
is how we compute the inner product of two vectors, and if you recall, the inner product is just another name for the dot product !
Note that


Given two vectors  and
and 


The two equations are just different ways of expressing the same thing.
It is interesting to note that  is
is  , which means that this value determines the intersection of the line with the vertical axis.
, which means that this value determines the intersection of the line with the vertical axis.
Why do we use the hyperplane equation  instead of
instead of  ?
?
For two reasons:
- it is easier to work in more than two dimensions with this notation,
- the vector
 will always be normal to the hyperplane(Note: I received a lot of questions about the last remark.
will always be normal to the hyperplane(Note: I received a lot of questions about the last remark.  will always be normal because we use this vector to define the hyperplane, so by definition it will be normal. As you can see this page, when we define a hyperplane, we suppose that we have a vector that is orthogonal to the hyperplane)
will always be normal because we use this vector to define the hyperplane, so by definition it will be normal. As you can see this page, when we define a hyperplane, we suppose that we have a vector that is orthogonal to the hyperplane)
And this last property will come in handy to compute the distance from a point to the hyperplane.
Compute the distance from a point to the hyperplane
In Figure 20 we have an hyperplane, which separates two group of data.
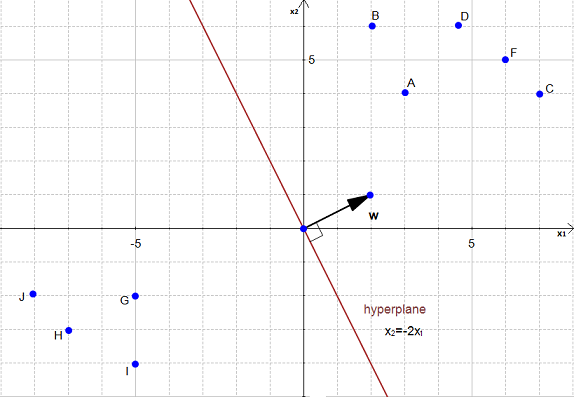
To simplify this example, we have set  .
.
As you can see on the Figure 20, the equation of the hyperplane is :


with  and
and 
Note that the vector  is shown on the Figure 20. (w is not a data point)
is shown on the Figure 20. (w is not a data point)
We would like to compute the distance between the point  and the hyperplane.
and the hyperplane.
This is the distance between  and its projection onto the hyperplane
and its projection onto the hyperplane
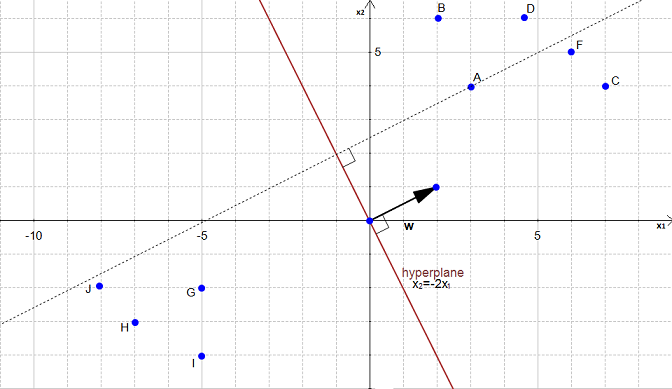
We can view the point  as a vector from the origin to
as a vector from the origin to  .
.
If we project it onto the normal vector 
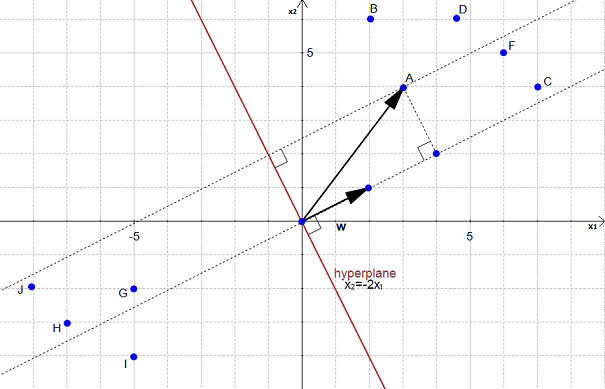
We get the vector 
Our goal is to find the distance between the point  and the hyperplane.
and the hyperplane.
We can see in Figure 23 that this distance is the same thing as  .
.
Let's compute this value.
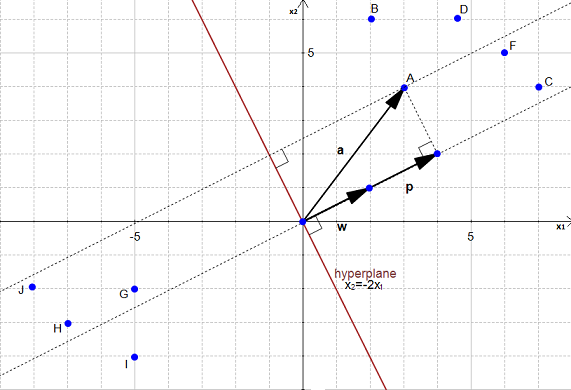
We start with two vectors,  which is normal to the hyperplane, and
which is normal to the hyperplane, and  which is the vector between the origin and
which is the vector between the origin and  .
.

Let the vector  be the direction of
be the direction of 

 is the orthogonal projection of
is the orthogonal projection of  onto
onto  so :
so :








Compute the margin of the hyperplane
Now that we have the distance  between
between  and the hyperplane, the margin is defined by :
and the hyperplane, the margin is defined by :

We did it ! We computed the margin of the hyperplane !
Conclusion
This ends the Part 2 of this tutorial about the math behind SVM.
There was a lot more of math, but I hope you have been able to follow the article without problem.
What's next?
Now that we know how to compute the margin, we might want to know how to select the best hyperplane, this is described in Part 3 of the tutorial : How to find the optimal hyperplane ?
I am passionate about machine learning and Support Vector Machine. I like to explain things simply to share my knowledge with people from around the world.
