This is the Part 5 of my series of tutorials about the math behind Support Vector Machines.
Today we are going to study convex functions.
If you did not read the previous articles, you might want to start the serie at the beginning by reading this article: an overview of Support Vector Machine.
How can we find a global minimum?
There is one simple way to find the global minimum:
- Find all the local minima
- Take the smallest one; it is the global minimum.
Another approach is to study the function we are trying to minimize. If this function is convex, then we are sure its local minimum is a global minimum.
Theorem: A local minimum of a convex function is a global minimum (Proof page 9)
Convex functions
What is a convex function?
A function is convex if you can trace a line between two of its points without crossing the function line.
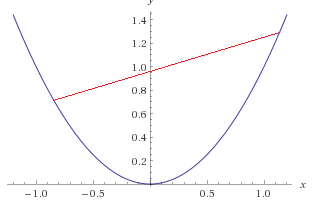
However, if you cross the function line, then the function is non-convex.
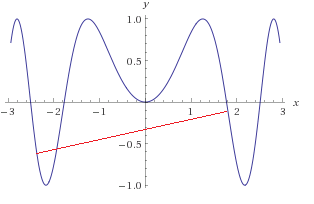
As you can see in the figure above, the red line crosses the function, which means it is non-convex. Note, however, that the function is convex on some intervals, for instance on [-1,+1].
You can read about a more rigorous definition of a convex function here. But from now what is important to understand is that it is easy to find the global minimum of a convex function.
As often, there is also an "opposite" concept: a function  is concave if
is concave if  is convex.
is convex.
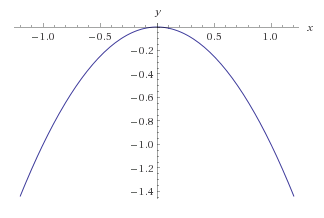
The problem here is that my original definition of a convex function is also true, I can trace a line between two points of the function without crossing the line...
So the mathematicians have been a little bit more specific, and they say that:
A function is convex if its epigraph (the set of points on or above the graph of the function) is a convex set.
But what is a convex set?
In Euclidean space, a convex set is the region such that, for every pair of points within the region, every point on the straight line segment that joins the pair of points is also within the region. (Wikipedia)
We use the same logic as before. A set of points is convex if when we pick two points belonging to the set and we trace a line between them then the line is inside the set.

If you guessed right, the circle and the triangles are convex sets. In the figure below I traced a red line between two points. As you can see, the line joining two points of the star leave the figure indicating that it is not a convex set.

We can now use this knowledge to determine if a function is convex.
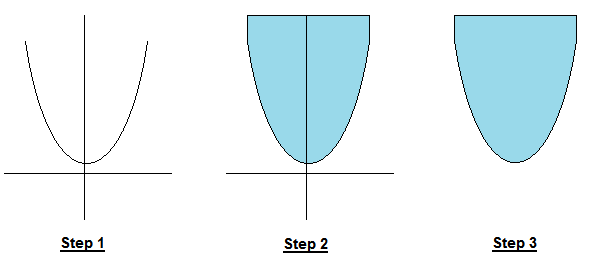
Step 1: We have a function and we wish to know if it is convex
Step 2: We take its epigraph (think of it as filling it with water but the water cannot overflow so it adds up vertically when it reaches the limits of the function)
Step 3: If the shape of the epigraph is convex, then it is a convex function!
How do we know if a function is convex?
The definition with the epigraph is simple to understand, but with functions with several variables it is kind of hard to visualize. So we need to study the function:
More generally, a continuous, twice differentiable function of several variables is convex on a convex set if and only if its Hessian matrix is positive semidefinite on the interior of the convex set. (Wikipedia)
If we want to check if a function is convex, one easy way is to use our old friend the Hessian matrix. However, instead of checking if it is positive definite as we did in the previous article, this time, we need to check if it is positive semidefinite.
What is the difference?
Theorem:
The following statements are equivalent:
- The symmetric matrix
 is positive semidefinite.
is positive semidefinite. - All eigenvalues of
 are non-negative.
are non-negative. - All the principal minors of
 are nonnegative.
are nonnegative. - There exists
 such that
such that 
(Source)
As before we will use the minors. The difference here is that we need to check all the principal minors, not only the leading principal minors. Moreover, they need to be nonnegative. (A number is positive if it is greater than zero. A number is non-negative if it is greater than or equal to zero).
Example: is the banana function convex?
We saw that the Hessian of our banana function was:

Its principal minors of rang 1 are:
 is
is  (we removed line 1 and column 1).
(we removed line 1 and column 1).
 is
is  (we removed line 2 and column 2).
(we removed line 2 and column 2).
If the function is convex, these minors should be nonnegative on the interior of the convex set. Which convex set? By definition, the domain of a convex function is a convex set. In our case when we say that a function is convex on a convex set, we are talking about its domain.
The restriction "on the interior" tells us that we should not pick points which are on the border of the set.
In our example, the function is defined in  which is a convex set. So we would need to prove that for any point we pick the principal minors are nonnegative.
which is a convex set. So we would need to prove that for any point we pick the principal minors are nonnegative.
We see that that minor  is always positive. However, we can easily find a point for which
is always positive. However, we can easily find a point for which  is negative. For instance for the point
is negative. For instance for the point 
 .
.
As a result, we can tell the banana function is not convex.
It turns out there are several ways to prove that a function is convex. For more guidelines on the subject, refer to this paper, part 2.1.
Why are convex functions so cool?
First, we saw that the local minimum of a convex function is a global minimum. It is a pretty good result to help us find a solution more quickly.
Moreover, in general, convex optimization problems are easier to solve. Why?
To get a better idea let us look at some figures.
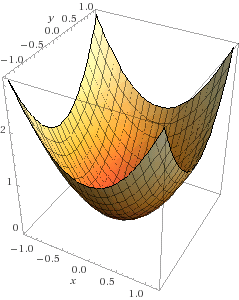
Imagine that solving the optimization problem is like throwing a marble onto a surface. In the case of the convex surface, like the one in the figure above, no matter where you put the marble, it will go directly to the center of the bowl which is the minimum of the function.
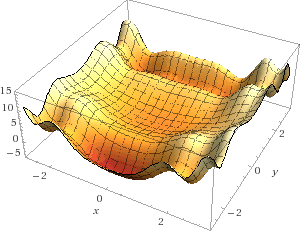
What if the surface is non-convex? Well as you can see throwing a marble randomly onto the surface has very few chances of hitting the global minimum. Instead, it is likely that the marble will fall into one of the many local minima. And when this is the case, what do you do? Do you try to push the marble to get somewhere else? As you can see, the problem is much more complicated.
The marble analogy is interesting because it is basically what does an optimization algorithm called gradient descent. Another way to solve an optimization problem is to use the well-known Newton's method. I encourage the interested reader to study these methods in detail and even to try implementing them.
Conclusion
In this part, we learned what a convex set is and how to tell if a function is convex. Moreover, we saw a visual representation showing us why convex optimization is usually much simpler than non-convex optimization: because there are no local minima.
Convexity is an important concept to understand when studying optimization. Now that we know it better, we will see another important aspect called "duality". Eventually, we will see how we can solve more difficult optimization problems. Go read the Part 6 of this tutorial series to find out! Thanks for reading.
I am passionate about machine learning and Support Vector Machine. I like to explain things simply to share my knowledge with people from around the world.